12. Advanced concepts

12.1. Integration methods

Differential equations may be solved using several methods that can be selected with the DifferentialEquation.select() method of the differential equation object. Below is the description of each method.

12.1.1. Forward Euler

Considering an equation of the form $x' = f(x)$ , $x$ is updated according to:

$x \leftarrow x + f(x) \times dt$

12.1.2. Runge-Kutta second order

Considering an equation of the form $x' = f(x)$ , $x$ is updated according to:

$k_1 &= f(x) k_2 &= f(x + x dt) x &= x + \frac{1}{2}(k_1 + k_2) dt$

12.1.3. Runge-Kutta fourth order

Considering an equation of the form $x' = f(x)$ , $x$ is updated according to:

$k_1 &= f(x) k_2 &= f(x + \frac{1}{2} k_1 dt) k_3 &= f(x + \frac{1}{2} k_2 dt) k_4 &= f(x + \frac{1}{2} k_ 3dt) x &\leftarrow x + \frac{1}{6}(k_1 + k_4) dt + \frac{1}{3}(k_2 + k_3) dt$

12.1.4. Exponential Euler

Considering an equation of the form $x' = f(x)$ , $x$ is updated according to:

$x \leftarrow x + x e^{-Ddt} + \frac{A}{B} (1 - e^{-D*dt})$

12.2. Asynchronicity

Most computational paradigms linked to artificial neural networks (using rate code) or cellular automata use implicitly what is called synchronous evaluation of activity. This means that information at time t+dt is evaluated exclusively on information available at time t. The explicit numerical procedure to perform such a synchronized update is to implement a temporary buffer at the unit level where activity computed at time 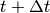$t + \Delta t$ is stored. Once all units have evaluated their activity at time 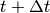$t + \Delta t$ , The current activity is replaced by the content of the buffer. 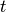We point out that other update procedures have been developed [Lambert:1991] but the basic idea remains the same, namely not to mix information between time $t$ and time 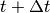$t + \Delta t$ . To perform such a synchronization, there is thus a need for a global signal that basically tell units that evaluation is over and they can replace their previous activity with the newly computed one. At the computational level, this synchronization is rather expensive and is mostly justified by the difficulty of handling asynchronous models.

For example, cellular automata have been extensively studied during the past decades for the synchronous case and many theorems has been proved in this context. However, some recent works on asynchronous cellular automata showed that the behavior of these same models and associated properties may be of a radical different nature depending on the level of synchrony of the model (you can asynchronously evaluate only a subpart of all the available automata). In the framework of computational neuroscience we may then wonder what is the relevance of synchronous evaluation since most generally, the system of equations is supposed to give account of a population of neurons that have no reason to be synchronized (if they are not provided with an explicit synchronization signal).

In [Taouali:2009] and [Rougier:2010], we’ve been studying the effect of such asynchronous computation (uniform or non-uniform) on neural networks and more specifically for the case of dynamic neural fields. The whole story is that if you choose a 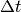$\Delta t$ small enough, asynchronous and synchronous computation may be considered to lead tp the same result provided the leak term in your equation is not too strong. This is reason why currently, the asynchronous part of dana has been disabled.

12.2.1. References

[Lambert:1991]

J.D. Lambert, « Numerical methods for ordinary differential systems: the initial value problem », John Wiley and Sons, New York, 1991.

[Rougier:2010]

NP. Rougier and A. Hutt, « Synchronous and Asynchronous Evaluation of Dynamic Neural Fields », Journal of Difference Equations and Applications, to appear.

[Taouali:2009]

W. Taouali, F. Alexandre, A. Hutt and N.P. Rougier, « Asynchronous Evaluation as an Efficient and Natural Way to Compute Neural Networks », 7th International Conference of Numerical Analysis and Applied Mathematics - ICNAAM 2009 1168, pages. 554-558.

12.3. Finite transmission speed connection

So far, we’ve been only considering infinite transmission speed from one group to the other. While this simplify computations a lot, it may not be satisfactory if one wants to consider the effect of a finite transmission speed in connection. We’ve been studying in [HuttRougier:2010] the spatio-temporal activity propagation which obeys an integral-differential equation in two spatial dimensions that involves a finite transmission speed, i.e. distance-dependent delays and derived a fast numerical scheme that allow to quickly simulate numerically such equations.

More formaly, the NF equation reads:

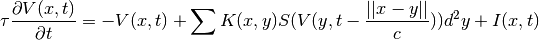
$\tau \frac{\partial{V}(x,t)}{\partial{t}} = -V(x,t) + \sum K(x,y) S(V(y, t- \frac{||x-y||}{c})) d^2 y + I(x,t)$

where:

V(x,t) is the potential of a neural population at position x and time t

We proposed a fast algorithm for simulating such an equation but it has not been integrated into dana yet.

12.3.1. References

[HuttRougier:2010]

A. Hutt and N.P. Rougier, « Activity spread and breathers induced by finite transmission speeds in two-dimensional neural fields**Emergence of Attention within », Physical Review Letter E, 2010.

Prev	1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16	Next
11. Examples	Home	13. Application Programming Interface