
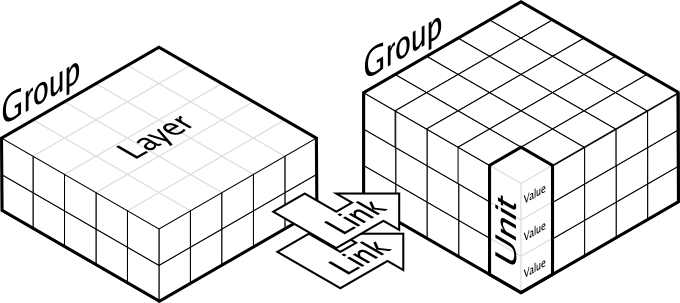
Computational neuroscience is a vast domain of research going down from the very precise modeling of a single spiking neuron, taking into account ion channels and/or dendrites spatial geometry up to the modeling of very large assemblies of simplified neurons that are able to give account of complex cognitive functions. Dana attempts to address this latter modeling activity by offering a python computing framework for the design of very large assemblies of neurons using numerical and distributed computations. The computational paradigm supporting the dana framework is grounded on the notion of a unit that is a essentially a set of arbitrary values that can vary along time under the influence of other units and learning. Each unit can be connected to any other unit (including itself) using a weighted link and a group is a structured set of such homogeneous units.
More formally, we can write the following definitions:
The dana framework offers a set of core objects needed to design and run such models. However, what is actually computed by a unit and what is learned is the responsibility of the modeler who is in charge of describing all equations governing the behavior of units groups and connections over time and learning.
Let us consider how learning takes place in the multi-layer perceptron with the back-propagation learning rule. This learning rule requires first to compute the activities of each layer in a feed-forward way (to get the output) and then to apply the learning rule backwards. This implicitly requires a supervisor that is able to coordinate the different layers between them, to compute the error between the obtained and desired output and to back-propagate it. The problem, in our sense, is that this supervisor has not been made explicit and has not been instantiated within the model (e.g. by a group of dedicated neurons). This means that part of the properties of the system are indeed introduced by the supervisor, without specifying how the supervisor itself is controlled. This also means that one would not be able to reproduce this network using, for instance, only hardware artificial neurons linked together without introducing an ad-hoc surrounding architecture for the coordination of the network. More generally, this kind of artefact is widely spread in the connectionnist and computational neuroscience literature. The question is to decide to what extent these artefacts can impact results and claims. We will not answer the general case, but, in the context of the study of emergence, we want to strongly constrain our modeling framework such that we won’t have such artefacts and what may emerge from our models may be considered a a real emergent property of the model.
Dana has been designed in the first place for computational neurocience. However, because of the structure of the framework, it might be possible to use dana other scientific modesl as well. You might for example have a look at the Examples chapter that introduces models dealing with cellular automaton and image processing.
If you model possess something like a central supervisor or any kind of ordered evaluation, then you cannot use DANA to implement your model. As explained in the introduction, DANA makes no distinction between groups and they are evaluated in random order. Because of this restriction, you cannot for example implement a multi-layer perceptron (because of the feed-forward evaluation and backward learning) or a Kohonen network (because of the central supervisor deciding which unit won the competition).